Series numéricas
Hasta ahora teníamos entendido que una sucesión es un conjunto ordenado de números que respetan algún criterio, pero ahora debemos aprender a diferenciarlo de las series. Una serie es la sumatoria infinita de una sucesión (representado por la letra griega ∑), es decir, la suma de todos sus términos.
Seguramente dirás que teníamos una fórmula para sumar las sucesiones aritméticas y geométricas, y la verdad es que sí pero en este caso no utilizaremos esas fórmulas ya que la suma de una serie no es una suma (en el sentido aritmético) sino un límite de sumas.
La suma de las series se clasifican en convergentes y divergentes. Decimos que la suma de una serie convergente cuando podemos obtener un valor numérico al hallar el límite de la sucesión de sumas parciales, en cambio cuando el resultado es divergente, el límite tenderá a infinito.
Si la sucesión de sumas parciales carece de límite, la serie se llama oscilante.
Series especiales
Existen dos tipos de series que tendremos que considerar para diferenciarlas:
- Serie geométrica: Una serie geométrica será la suma parcial de los términos de una progresión geométrica. Es decir, una serie geométrica tendrá la siguiente forma:

r (razón) puede ser tanto positiva como negativa y dependiendo el valor de la misma, podemos clasificar la serie de la siguiente manera:
- |r| < 1 , r^n disminuye en valor numérico cuando n aumenta por lo cual el límite cuando n tiende a infinito de r^n dará 0 y en consecuencia, la serie converge. Si es asi, es posible hallar la suma de términos de esta serie:

- |r| >1, r^n se hará infinito cuando n aumenta indefinidamente, por lo tanto la suma de términos se hará infinita, en consecuencia la serie diverge.
- r=-1, este es un caso especial ya que la serie será: a -a + a - a + a......
Si n es par, la suma es cero. Si n es impar, la suma es a. Cuando n aumenta indefinidamente la suma no aumenta indefinidamente y no tiende hacia un límite, esto quiere decir que será divergente. Una serie de esta clase se llama oscilante.
Veamos unos ejemplos donde se visualiza este criterio:

- Serie armónica: Llamaremos "serie armónica" a la serie que presenta la siguiente característica:

- Serie armónica generalizada o serie "p": Este tipo de serie son conocidas por su expresión general:

Ya está analizado el caso del exponente p=1, el cual corresponde a la serie armónica, por lo que se puede analizar qué sucede si p ≠1:
- Si p>1 la serie convergerá.
- Si p≤1 la serie divergerá.
Este tipo de serie se puede utilizar de manera frecuente junto al criterio de comparación que veremos más adelante ya que en estas series es fácil analizar su convergencia sólo considerando su exponente, luego resulta sencillo en algunos casos utilizarlas para comparar con otras series que se quieran analizar.
- Serie telescópica: una serie telescópica es aquella serie cuyas sumas parciales poseen un número fijo de términos tras su cancelación. El nombre "telescópica" se debe a que si desarrollamos su suma parcial los sumandos se van cancelando de a dos. Tiene la siguiente característica:
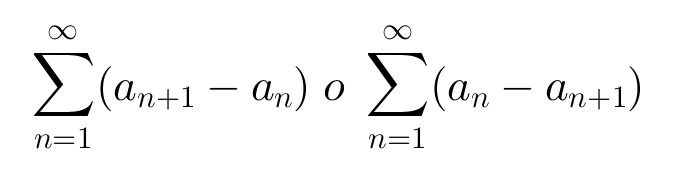
Y puede ser convergente o divergente según la tendencia de su suma. Muchas veces este tipo de series aparecen, por ejemplo de la siguiente manera:

Para poder resolver y analizar este tipo de series, debemos utilizar las sumas parciales y poder analizar la tendencia de su suma:

Si analizamos su suma parcial obtendremos lo siguiente: 1-1/2+1/2-1/3+1/3-1/4+1/4-1/5....
Lo que nos lleva a pensar que el resultado de su suma parcial será:

Criterios de convergencia
No todas las series son telescópicas, geométricas o armónicas, por lo cual podremos utilizar diversos criterios de convergencias para analizar si la serie converge o no. La ventaja es que permiten analizar la convergencia o divergencia de la serie sin necesidad de tener la expresión de la suma parcial ya que se trabajará con la expresión del término que forma la serie. La debilidad es que sólo nos permite clasificarla, pero en caso de ser convergente no se conoce a qué valor converge la suma.
Los criterios que podemos utilizar son los siguientes:
- Criterio de comparación: Se utiliza para series minorantes y mayorantes. Para poder utilizarlo las series a comparar no deben tener términos negativos. Este criterio consiste en comparar una serie, que no sabemos si es convergente o divergente, con otra que ya sabemos qué tipo es.
Si sabemos que Σ bn converge y queremos demostrar que Σ an converge, basta con demostrar que an<bn.
En cambio si sabemos que Σ bn diverge y queremos demostrar que Σ an diverge, basta con demostrar que an>bn. Seguramente te preguntarás cómo hacerlo, pues es muy fácil, reemplazas los términos y comienzas a despejar hasta llegar a una desigualdad lógica. Veamos un ejemplo:

- Criterio de D'Alembert:
- Criterio de la integral:
- Criterio de Cauchy:
- Criterio de Leibniz:
